More experimentation in NNUE
Hi! Since last time I've done a little work on bullet, adding some new LR schedulers and allowing for the use of test datasets. I also ran a big guantlet on my old net scaling experiments, and talked to some friends about their results with different adjustments to their main-run training pipelines. I also merged a new main network to Viridithas, which I'll talk a little bit about first.
New net
Viridithas's previous neural network, gestalt, was a one-layer MLP with
squared-clipped-relu activation, . It takes the
board (represented as a 768-element binary vector), and applies a
linear layer to generate a vector of pre-activations.
Notable (and common among neural networks for chess) is that it does this twice,
once for each "perspective", to generate two 1536-element vectors, which are then
concatenated (side-to-move first) into a single 3072-element vector, activated
with SCReLU, and then passed through a linear layer to
compute a position evaluation.
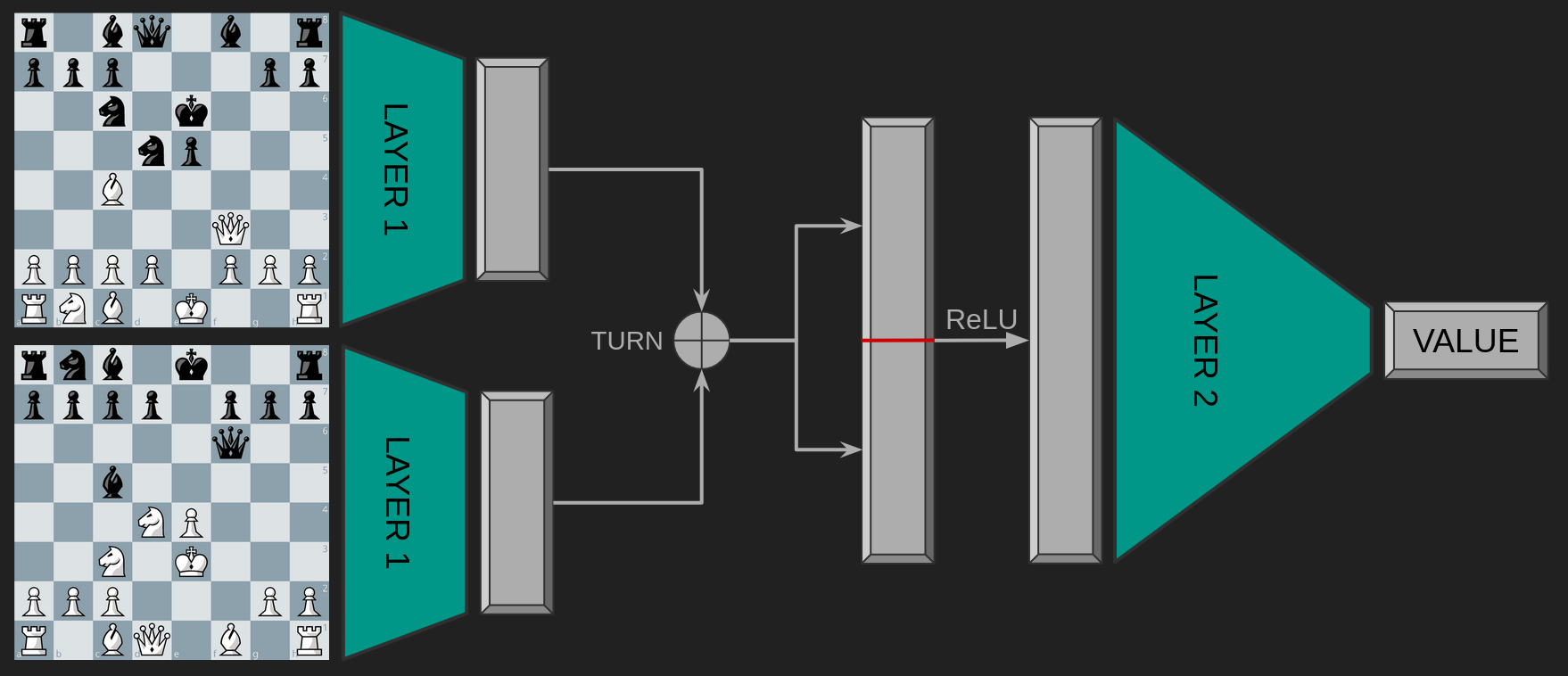
Simplified diagram to give an intuition for the structure of such networks.
These networks work extremely well, particularly because you can exploit their structure to efficiently update them across similar positions. An enhancement to this design is to switch out the first layer depending on some important and rarely-changing feature of the board. For most engines, this feature is the position of the king belonging to our perspective. This allows each version of the first layer to learn how to do a good job of generating the hidden state for only those king positions that it is assigned. For example, if you have a “bucket” allocated only to positions where “our king” is on the back rank of the chessboard, then this layer never has to waste time learning how to evaluate positions where we are using our king to guide a pawn to promotion, and can spend more time figuring out how to evaluate attacks against a castled king. This is technique is a form of Mixture of Experts, but where the gating function is not learned and instead uses a handcrafted heuristic that we know is important. Viridithas uses nine such experts in its main net.

An example mapping from square-sets to sub-networks. Squares with the same colour are handled by the same network when our king is on those squares.
Viridithas's new net employs a similar approach for the final layer, this time switching between eight subnetworks based on the number of pieces on the board. It also uses a significantly larger dataset. One might think that nine first-layer experts and eight second-layer experts could be problematic, as there are now expert combinations that have to be trained to work together. Thankfully, because these networks are switched out and combined, and because they all have to pass through the same activation bottleneck, they are automatically regularised to cope with the same representation space and data requirements do not increase to a degree that is problematic.
Scaling
During the tests I did last month, I trained a large number of networks across a wide range of scales. I noted that they predictably improved upon loss as they scaled up, but note: loss is not the interesting metric! Indeed, it matters not how well a network approximates the training distribution, but how well it performs when integrated within a chess engine. As such, I took ten networks, from 32 neurons all the way up to 4096 neurons, and ran them in a fixed-nodes guantlet for 11000 games to determine how Elo scales with network size. The results are as follows, plotted alongside the final losses that these networks achieved, scaled to make the relationship clear:
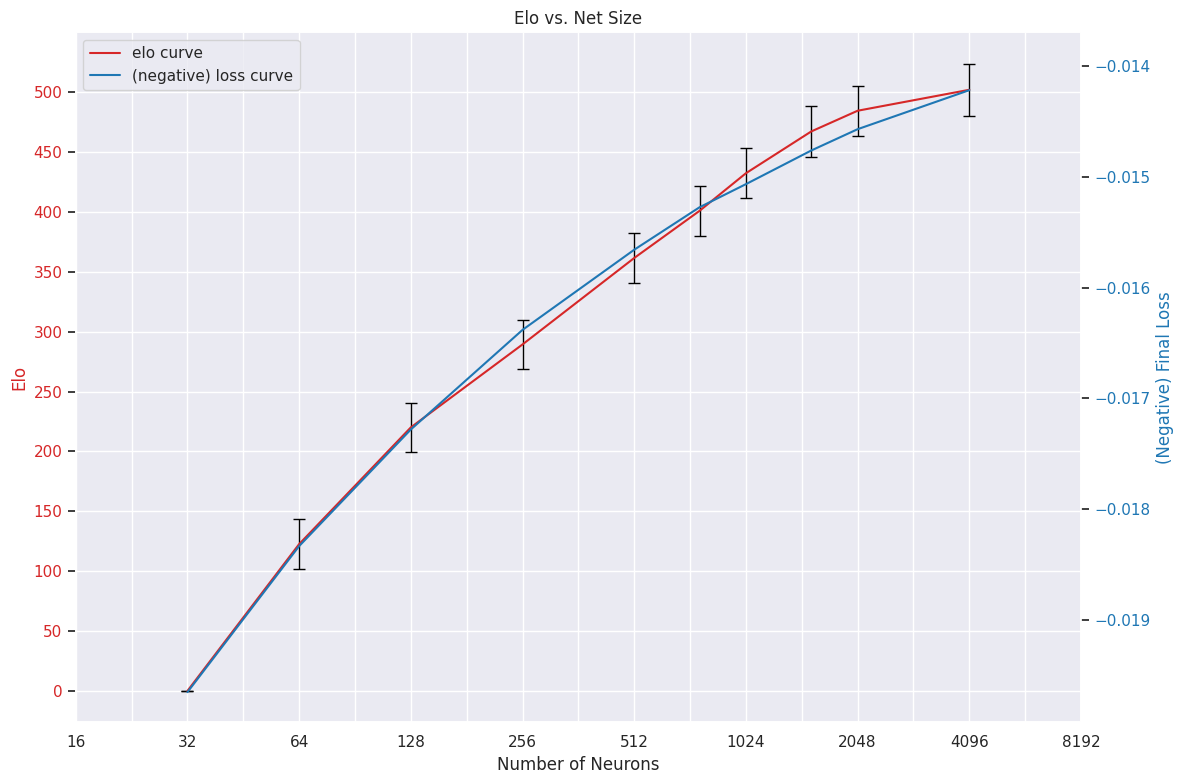
Elo appears to track fairly closely with final loss.
This is one of those graphs that sort of just confirms what everyone suspected already, but it's nice to know.
Community results
Several others in the engine programming community have been testing variations on the network training pipeline, and getting mixed results. I report on them here, for the sake of collecting knowledge into a more accessible format.
Alternative optimisers
The community has experimented with optimisers other than the tried-and-tested AdamW, with mixed success.
Ranger21
Ranger21 (code, paper) is an optimiser that combines AdamW with many different improvements aggregated from the deep learning literature. Programmer zzzzz tested it in their engine Starzix and found poor results in three tests with different learning-rate configurations:
1 2 3 4 5 6 | |
1 2 3 4 5 6 | |
1 2 3 4 5 6 | |
Lion
Lion (code, paper) is another optimiser, that was discovered by program search. Similarly poor results were found by zzzzz:
1 2 3 4 5 6 | |
Varying AdamW parameters
AdamW has several hyperparameters. Engine developer martinn found success in Motor by tweaking the beta1 parameter from 0.9 to 0.95:
1 2 3 4 5 6 | |
Tighter weight clipping for better quantisation
As I mentioned in my post on performance optimisation for NNUE, the range of values that the network weights can take on is very important for writing efficient SIMD code for quantised networks. In order to allow for larger quantisation constants (and hence less quantisation error), martinn experimented with tightening the weight clipping constants used during training, lowering the bound on the absolute value of the weights, and correspondingly allowing proportionally larger quantised weights. This worked well in Motor. At short time control:
1 2 3 4 5 6 | |
and at long time control:
1 2 3 4 5 6 | |
Modifications to mean-squared-error
By default, the loss used for training these efficiently-updatable neural networks is a mean-squared-error loss on the tanh activation of the final layer against a target constructed by blending local search evaluation and the Win/Draw/Loss outcome from the position in question. It is possible to instead use different exponents for this loss, and in this case several engines experimented with raising the error to the power of , rather than using squared error. The effect of this is to punish large errors more strongly, while punishing smaller errors less. This worked well across two different engines.
In Starzix:
1 2 3 4 5 6 | |
and in Motor:
1 2 3 4 5 6 | |
Applying these results all at once
Using a higher beta1 in AdamW appears to be worth ~ Elo, alternative quantisation ~ Elo, and modified loss ~ Elo. Clearly, the composition of these three techniques should be an easy improvement in my chess engine, Viridithas! Not so quick.
At fixed-nodes (where the engine searches the same small number of positions each move) the change appears to be an obvious and significant winner:
1 2 3 4 5 6 | |
At short time control, this gain decays quite significantly (but is still convincing!):
1 2 3 4 5 6 | |
Unfortunately, at long time control, this patch becomes indistinguishable from neutral. This leads me to believe that this might actually begin to scale to negative Elo at longer time control.
1 2 3 4 5 6 | |
Disappointing. Well, that's all. See you in the next one!