NNUE Performance Improvements

This document lists and describes performance improvements that are applicable to efficiently updatable neural networks in chess engines.

As a primer, I will quickly explicate the functioning of these networks. I will not cover the mathematical theory, which is better described by the author of the Bullet NNUE trainer, here. These networks invariably make use of float-to-integer quantisation of parameters, allowing floating-point calculations to be approximated in integer arithmetic, with two main benefits - first, integer arithmetic is somewhat faster than floating-point, and second, one can quantise from float32 down to int16 (or even int8), allowing for SIMD (Single-Instruction Multiple-Data) CPU instructions to operate on a larger number of neuron activations at once.

Representation of how values are packed into SIMD registers:

(image credit to McYoung, © 2024 Miguel Young de la Sota)

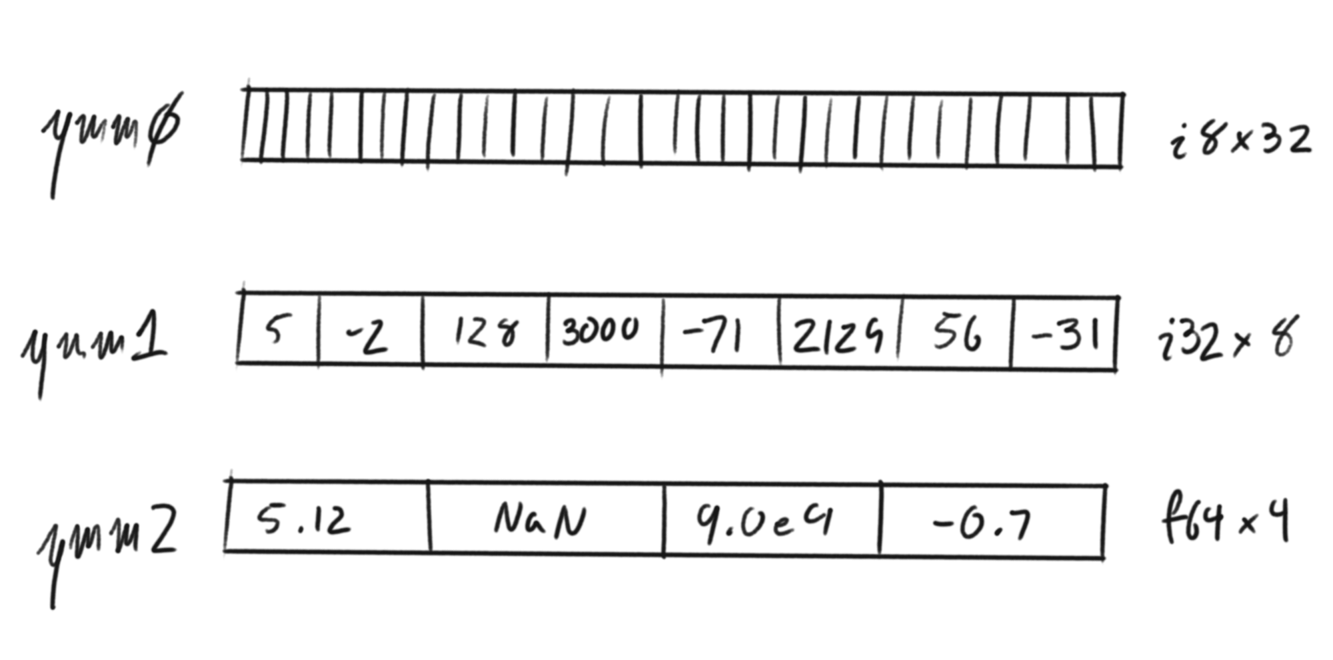
Important Components of an NNUE System

The Accumulator

The whole point of NNUE is to incrementally modify an internal state of neural activations - specifically, the activations of the very first layer. These incrementally-updated activations are stored in an array called an accumulator.

It is possible to maintain such a structure efficiently because the input features of NNUE are entirely binary[^1], and so whenever a feature changes we can simply add or subtract a component of the feature transformer matrix to generate a new accumulator from an old one.

We also avoid the need to do any activation when a feature changes, because the accumulator stores the pre-activation values of the neurons - if the output of a neuron is $f(x \cdot w + b)$, then the accumulator stores the values that are the inputs to the activation function $f$.

Hopefully this diagram should make it clearer as to what's going on:

And here's corresponding code for adding a certain feature to an accumulator state:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

/// Add a feature to a square.
/// Modifies `accumulator` in-place.
fn vector_add_inplace(
    accumulator: &mut [i16; LAYER_1_SIZE],
    ft_weights: &[i16; INPUT * LAYER_1_SIZE],
    feature_idx_add: usize,
) {
    // get the offset into the feature transformer weights
    let offset_add = feature_idx_add * LAYER_1_SIZE;
    // get the section of the matrix corresponding to this feature
    let a_block = &ft_weights[offset_add..offset_add + LAYER_1_SIZE];
    // add the weights to the accumulator
    for (i, d) in accumulator.iter_mut().zip(a_block) {
        *i += *d;
    }
}

So, for example, if you wanted to tell the network that a white knight has appeared on E3, then you'd run

1
2

let white_knight_e3 = Colour::White * COLOUR_STRIDE + PieceType::Knight * PIECE_STRIDE + Square::E3;
vector_add_inplace(&mut network.current_accumulator, &NNUE.ft_weights, white_knight_e3);

[^1]: Technically, this would work with trinary inputs of the form $\{-1, 0, 1\}$, too.

The Output Layers

The layers after the feature transformer operate on non-binary inputs, and as such cannot benefit from efficient updates. As such, we are forced to make these layers few and small, with most engines employing only one post-FT layer that simply calculates the evaluation directly from the activated accumulator.

Fused Updates

Almost invariably, multiple feature updates are happening at once. There are three important cases: - a quiet move where a piece moves from some square to another square will incur two feature updates, one add and one subtract. - a capture involves three updates, two subtractions (captured piece and source square) and one addition (target square). - castling involves four updates, for the source/target squares of the rook and king.

We can take advantage of this fact, and can avoid needless interstitial operations on the accumulator memory by operating on these features all at the same time. This manifests in functions that perform multiple additions and subtractions of feature vectors on the accumulator at the same time, often with unwieldy names like multiAddAddSubSub.

This looks essentially the same as the feature code shown before, but uses different memory for the old and new accumulators, as we maintain a stack of such accumulators to ease move make/unmake.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

/// Add two features and subtract two features all at once.
fn vector_add2_sub2(
    input: &[i16; LAYER_1_SIZE],
    output: &mut [i16; LAYER_1_SIZE],
    bucket: &[i16; INPUT * LAYER_1_SIZE],
    feature_idx_add1: usize,
    feature_idx_add2: usize,
    feature_idx_sub1: usize,
    feature_idx_sub2: usize,
) {
    let offset_add1 = feature_idx_add1 * LAYER_1_SIZE;
    let offset_add2 = feature_idx_add2 * LAYER_1_SIZE;
    let offset_sub1 = feature_idx_sub1 * LAYER_1_SIZE;
    let offset_sub2 = feature_idx_sub2 * LAYER_1_SIZE;
    let a_block1 = &bucket[offset_add1..offset_add1 + LAYER_1_SIZE];
    let a_block2 = &bucket[offset_add2..offset_add2 + LAYER_1_SIZE];
    let s_block1 = &bucket[offset_sub1..offset_sub1 + LAYER_1_SIZE];
    let s_block2 = &bucket[offset_sub2..offset_sub2 + LAYER_1_SIZE];
    for i in 0..LAYER_1_SIZE {
        output[i] = input[i] - s_block1[i] - s_block2[i] + a_block1[i] + a_block2[i];
    }
}

And here is code for dispatching to these various functions depending on the sort of update we're looking to apply:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

pub fn materialise_new_acc_from(
    &mut self,
    pov_update: PovUpdate,
    create_at_idx: usize,
) {
    let (front, back) = self.accumulators.split_at_mut(create_at_idx);
    let src = front.last().unwrap();
    let tgt = back.first_mut().unwrap();

    match (src.update_buffer.adds(), src.update_buffer.subs()) {
        // quiet or promotion
        (&[add], &[sub]) => {
            apply_quiet(add, sub, pov_update, src, tgt);
        }
        // capture
        (&[add], &[sub1, sub2]) => {
            apply_capture(add, sub1, sub2, pov_update, src, tgt);
        }
        // castling
        (&[add1, add2], &[sub1, sub2]) => {
            apply_castling(add1, add2, sub1, sub2, pov_update, src, tgt);
        }
        (_, _) => panic!("invalid update buffer: {:?}", src.update_buffer),
    }
}

Lazy Updates

In some circumstances, it can be a waste to update the accumulator, as it will not actually end up being needed to evaluate a position. As such, it can be better to keep track simply of the features that have changed, and only to force accumulator materialisation when one gets to the point of actually calling evaluate().

Here's an example of code that manages the creation of new accumulators along the stack when an evaluation is actually needed:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

fn apply_lazy_updates(&mut self, board: &Board, view: Colour) {
    let mut curr_index = self.current_acc;
    loop {
        curr_index -= 1;

        if self.accumulators[curr_index].correct[view] {
            break;
        }
    }

    let pov_update = PovUpdate::colour(view);

    loop {
        self.materialise_new_acc_from(pov_update, curr_index + 1);

        self.accumulators[curr_index + 1].correct[view] = true;

        curr_index += 1;
        if curr_index == self.current_acc {
            break;
        }
    }
}

Bucket Accumulator Caching ("Finny Tables")

Often, NNUE architectures make use of a technique called "king buckets", or often colloquially just "buckets". This refers to a technique where the weights of the feature transformer layer are dynamically switched depending on the location of the king on the board. This is explained in significant detail here.

As a result, when the king "changes bucket", a total re-creation (or "refresh") of the accumulator is required, as a totally different set of weights are being used to calculate the accumulator. As such, it might seem like we cannot do incremental updates - but we can! By maintaining a cache with N_BUCKETS slots, we can record previously seen positions that satisfy the king position for a certain bucket, alongside accumulators for such positions. Then, when the time comes that the search is exploring moves that change the king bucket, and requests an evaluation of a position with a changed feature transformer, we can look up the corresponding entry in this accumulator cache, compute a feature-difference between the cached position and the position that we are trying to evaluate, and incrementally update from that position, instead of recreating our accumulator ex nihilo.

Example code for probing the cache is given - note that this probing function also populates the cache, and works even if the cache is filled with null positions. As such, no store_accumulator_for_position function is required.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

/// Stores last-seen accumulators for each bucket, so that we can hopefully avoid
/// having to completely recompute the accumulator for a position, instead
/// partially reconstructing it from the last-seen accumulator.
pub struct BucketAccumulatorCache {
    accs: [[Accumulator; BUCKETS]; 2],
    board_states: [[BitBoard; BUCKETS]; 2],
}

pub fn load_accumulator_for_position(
    &mut self,
    board_state: BitBoard,
    pov_update: PovUpdate,
    acc: &mut Accumulator,
) {
    let side_we_care_about = if pov_update.white { Colour::White } else { Colour::Black };
    let wk = board_state.piece_bb(Piece::WK).first();
    let bk = board_state.piece_bb(Piece::BK).first();
    let (white_bucket, black_bucket) = get_bucket_indices(wk, bk);
    let bucket = if side_we_care_about == Colour::White { white_bucket } else { black_bucket };
    let cache_acc = self.accs[bucket].select_mut(side_we_care_about);

    let mut adds = ArrayVec::<_, 32>::new();
    let mut subs = ArrayVec::<_, 32>::new();
    self.board_states[side_we_care_about][bucket].update_iter(board_state, |f, is_add| {
        let (white_idx, black_idx) = feature::indices(wk, bk, f);
        let index = if side_we_care_about == Colour::White { white_idx } else { black_idx };
        if is_add {
            adds.push(index);
        } else {
            subs.push(index);
        }
    });

    let weights = NNUE.select_feature_weights(bucket);

    simd::vector_update_inplace(cache_acc, weights, &adds, &subs);

    simd::copy(cache_acc, acc.select_mut(side_we_care_about));
    acc.correct[side_we_care_about] = true;

    self.board_states[side_we_care_about][bucket] = board_state;
}

Lizard SIMD for Squared Clipped ReLU

Neural networks use activation functions. These tend to be simple differentiable nonlinear functions that allow the network to approximate complex functions. In our networks, we typically use the Rectified Linear Unit, ReLU, and some derivatives thereupon. Advanced deep learning models tend to use smooth ReLU-enhancements like GELU or GLU variants, but these are generally too costly to compute for us. A consideration imposed by quantisation is that we have a fixed max activation size before we suffer integer overflow - generally $32767$, i16::MAX. As such, we employ clipped ReLU, $f(x) = clamp(x, 0, 1)$ to ensure that we avoid overflows. A further enhancement is squared clipped ReLU (SCReLU), $f(x) = clamp(x, 0, 1)^2$, which remains cheap to compute but provides valuable additional nonlinearity to the model, allowing our extremely shallow models to capture more of the dynamics of the data. Not all engine developers have found SCReLU an improvement over ReLU/CReLU, but many have seen strong results.

Squaring poses an additional problem over CReLU, that of integer overflow - if we quantise to, say, $Q_A = 255$, which is the default of many trainers, then implementing squared clipped ReLU naively as clamp(x, 0, QA).pow(2) * w forces the activation-weight multiplication to occur in i32s, as ${Q_A}^2 = 255^2 = 65025$, which is greater than i16::MAX.

A now-obsolete trick to mitigate this is to set $Q_A = 181$, the largest possible value of $Q_A$ for which ${Q_A}^2$ is still less than i16::MAX, but this suffers significantly from the accuracy losses inherent in quantisation, and this becomes particularly painful in longer time controls, where quality of evaluation becomes relatively more important than speed.

The author of the Lizard chess engine invented a scheme that allows us the best of both worlds - large $Q_A$ for high-accuracy evaluation, while still performing multiplication entirely in 16-bit.

The scheme is as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

// load a SIMD vector of inputs, x
let x: i16x16 = simd_load(inputs, index);
// compute the clipped ReLU of the inputs, v
let v: i16x16 = simd_min(simd_max(x, simd_zeroes()), simd_splat(QA));
// load the weights, w
let w: i16x16 = simd_load(weights, index);
// compute t = v * w in 16-bit
// this step relies on v being less than 256 and abs(w) being less than 127,
// so abs(v * w) is at most 255*126=32130, less than i16::MAX, which is 32767,
// so the output still fits in i16.
let t: i16x16 = simd_multiply_i16_truncating(v, w);
// compute v * t and accumulate horizontally into 32-bit
let p: i32x8  = simd_multiply_i16_into_i32(v, t);
// p can then be added to whatever running sum we have going, e.g.
sum = simd_add_i32(sum, p);

We inject the weight-multiply after the clipped ReLU and before squaring, so we can fit all of our work inside 16-bit multiplies!

Important point: the output weight $w$ in this code is guaranteed to be in $[-126, 126]$ as a result of weight clipping to $[-1.98, 1.98]$ of $Q_B$. The Motor chess engine had success with narrowing the weight clipping bounds to $[-1.27, 1.27]$ and correspondingly increasing $Q_A$ to $403$.

Register Juggling

When constructing an accumulator from the bucket-accumulator cache, we must do a reasonably large number of updates to an accumulator. The naive approach leads to needless loads/stores to the accumulator, when all subtractions and additions can be done piece-wise, only storing the full-updated values.

Consider the difference between

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

let subs = [4, 5, 1, -4, 8];
let adds = [-2, 3, 7, 9, 4];

let val = &mut some_memory_location;

for s in subs {
    *val -= *s;
}
for a in adds {
    *val += *a;
}

and

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

let subs = [4, 5, 1, -4, 8];
let adds = [-2, 3, 7, 9, 4];

let val = &mut some_memory_location;

let mut reg = *val;
for s in subs {
    reg -= *s;
}
for a in adds {
    reg += *a;
}
*val = reg;

The first implementation does "a load and a store" for every loop iteration, whereas the second implementation does one load and one store. Strictly, Rust's mutable-reference-uniqueness-guarantee should allow the first snippet to be optimised into the second[^2], but in NNUE inference we're typically working with unsafe calls directly to SIMD intrinsics where the compiler may perhaps be less able to slice through to see our intent.

As an attempt to make use of this optimisation, I made this modification to my in-place vector modification function, at the suggestion of Engine Programming user fireandice, author of Titan. Note that this version does a sort of hot-potato dance with multiple local variables all arranged in a vector, which has a number of elements that should fit entirely in SIMD registers. Making this work in a robust, architecture-generic fashion took a while, as shown in my results table:

This approach of explicitly forcing the use of N registers works in other areas of NNUE inference, but my experiments with applying it to the fused update code resulted in a small (~0.6%) slowdown. The final code for accumulator construction after this optimisation is as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

pub fn vector_update_inplace(
    input: &mut Align64<[i16; LAYER_1_SIZE]>,
    bucket: &Align64<[i16; INPUT * LAYER_1_SIZE]>,
    adds: &[FeatureIndex],
    subs: &[FeatureIndex],
) {
    const REGISTERS: usize = 16;
    const UNROLL: usize = Vector16::COUNT * REGISTERS;
    let mut registers = [unsafe { Vector16::zero() }; 16];
    for i in 0..LAYER_1_SIZE / UNROLL {
        let unroll_offset = i * UNROLL;
        unsafe {
            for (r_idx, reg) in registers.iter_mut().enumerate() {
                *reg = Vector16::load_at(input, unroll_offset + r_idx * Vector16::COUNT);
            }
            for &sub_index in subs {
                let sub_index = sub_index.index() * LAYER_1_SIZE;
                let sub_block = slice_to_aligned(bucket.get_unchecked(sub_index..sub_index + LAYER_1_SIZE));
                for (r_idx, reg) in registers.iter_mut().enumerate() {
                    let sub = Vector16::load_at(sub_block, unroll_offset + r_idx * Vector16::COUNT);
                    *reg = Vector16::sub(*reg, sub);
                }
            }
            for &add_index in adds {
                let add_index = add_index.index() * LAYER_1_SIZE;
                let add_block = slice_to_aligned(bucket.get_unchecked(add_index..add_index + LAYER_1_SIZE));
                for (r_idx, reg) in registers.iter_mut().enumerate() {
                    let add = Vector16::load_at(add_block, unroll_offset + r_idx * Vector16::COUNT);
                    *reg = Vector16::add(*reg, add);
                }
            }
            for (r_idx, reg) in registers.iter().enumerate() {
                Vector16::store_at(input, *reg, unroll_offset + r_idx * Vector16::COUNT);
            }
        }
    }
}

[^2]: As proof that rustc can in fact achieve this, see this godbolt example.

TT Static Evaluation Caching