ANNUEP: Initial results

23 days ago, I began working on the Advanced NNUE Program. I remain aware of how self-aggrandising this name is.

In the intervening period, I have merged some minor enhancements to the Bullet NNUE trainer, which are instrumentally useful for the project. These are a graphing utility for plotting loss curves, and an improved implementation of learning rate scheduling.

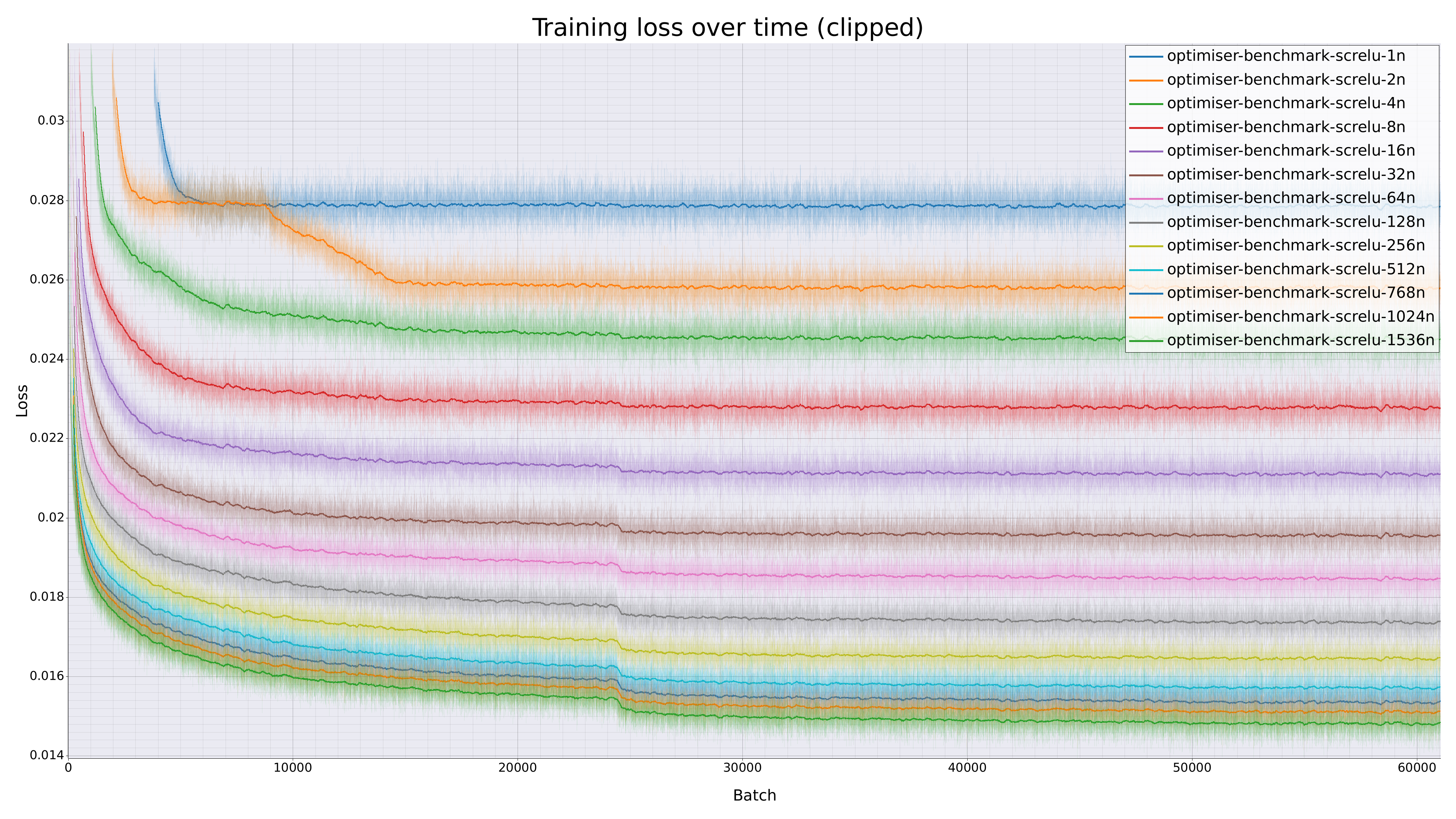
Loss curves for simple NNUEs as we scale up the hidden layer.

Work on Viridithas's NNUE implementation has been minor, I have only made minor cleanups to SIMD-accelerated copying, namely removing it.

Testing has been conducted on the newest batch of data that Viridithas has generated, a mix of seven different datagen runs, some with access to 6-piece tablebases and some without.

Tests conducted so far have been exploratory and rudimentary - I am not yet testing the trained networks in actual games of chess, nor am I recording loss on a test set. The former is a real issue, and I plan to do large-scale gauntlets soon, but I argue that the latter point is not actually a problem. Why? - these networks are small, are trained on billions of examples, are trained with regularising weight decay, and (in the current test configuration) see each datapoint only a single time. This is enough for me to be reasonably confident that overfitting is not occurring - though I intend to add support for test/train split to Bullet anyway, for my peace of mind.

Anyway, on to the initial results:

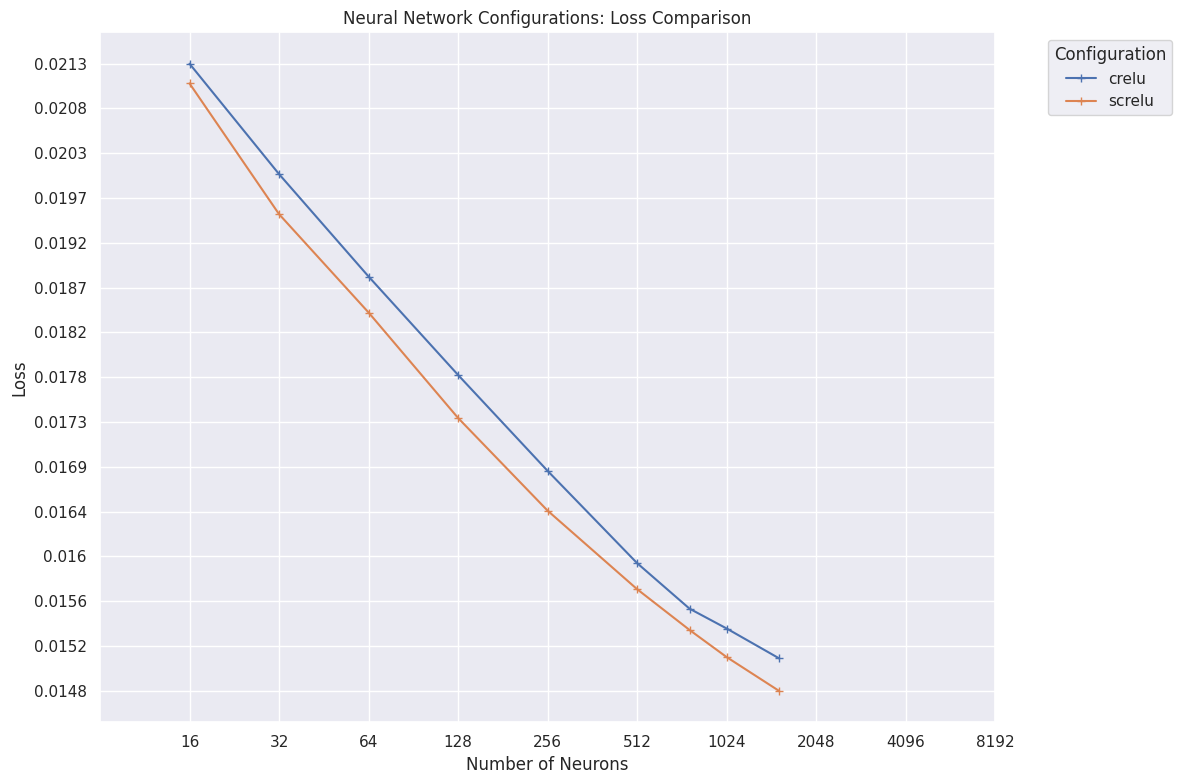
Final losses achieved after 10 superbatches of NNUEs with crelu and screlu activation, grouped by hidden layer neuron count.

Compare crelu (blue) with screlu (orange). Squared clipped ReLU dominates clipped ReLU across all configuations, and at higher neuron counts the loss difference is so stark as to make SCReLU activation worth almost the same as a 50% network size increase - the 1536-neuron CReLU net achieves the same final loss as the 1024-neuron SCReLU net. This is surpringly concordant with some of the activation-function research in large-scale deep learning, particularly the Primer language-modelling paper:

Primer's improvements can be mostly attributed to two simple modifications: squaring ReLU activations and adding a depthwise convolution layer after each Q, K, and V projection in self-attention.

These results make sense, as many chess engines have found that switching to SCReLU from CReLU yields Elo gains in the double-digits.

Some more tenuous results originate from varying batch-size:

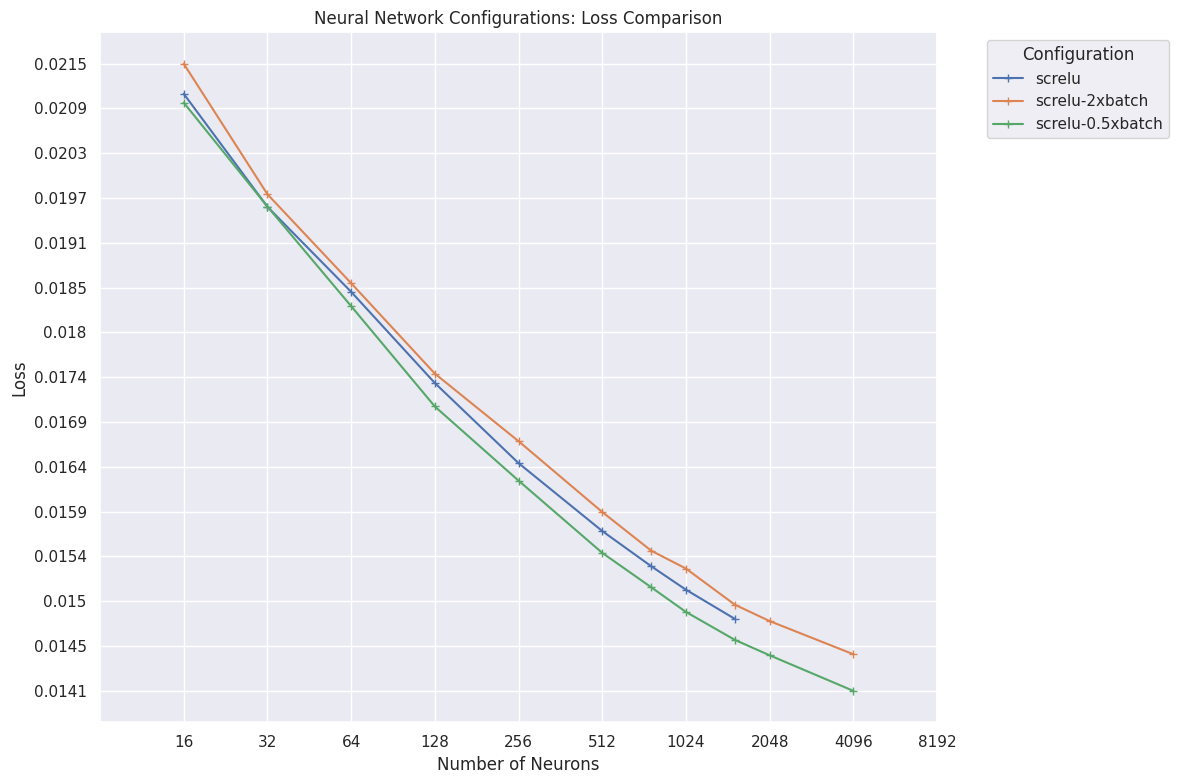
Final losses achieved after 10 superbatches with screlu activation, varying batchsize, grouped by hidden layer neuron count.

Here we vary batch-size in $\{8192,16384,32768\}$ while holding the total number of training examples fixed, by correspondingly halving or doubling the number of batches per super-batch. These results appear to show that smaller batches train more efficiently per unit compute (no significant difference in training speed was observed between batch-sizes). On this evidence, I suggested that the author of Alexandria try training a net with his usual configuration, but while halving his batchsize and correspondingly doubling the number of batches per super-batch. Unfortunately, this was not successful. There are a number of potential explanations for this:

1. Loss on the dataset simply does not cleanly translate into Elo. (unlikely, when the configurations are so similar)
2. Small batch-sizes are worse when the training run is much longer - Alexandria trains for 800 super-batches, far more than the 10 that were used to generate these results.
3. Large batch-sizes (while they achieve worse loss) somehow regularise the network, resulting in better generalisation behaviour to OOD positions in actual play. This is contrary to the usual wisdom of Keskar et al. [2017].

   It has been observed in practice that when using a larger batch there is a degradation in the quality of the model, as measured by its ability to generalize. We investigate the cause for this generalization drop in the large-batch regime and present numerical evidence that supports the view that large-batch methods tend to converge to sharp minimizers of the training and testing functions - and as is well known, sharp minima lead to poorer generalization. In contrast, small-batch methods consistently converge to flat minimizers, and our experiments support a commonly held view that this is due to the inherent noise in the gradient estimation.

4. Some other thing is going on that makes the Alexandria configuration meaningfully different from mine.

Now, some other results - output buckets are a modest but clear improvement over a single output layer:

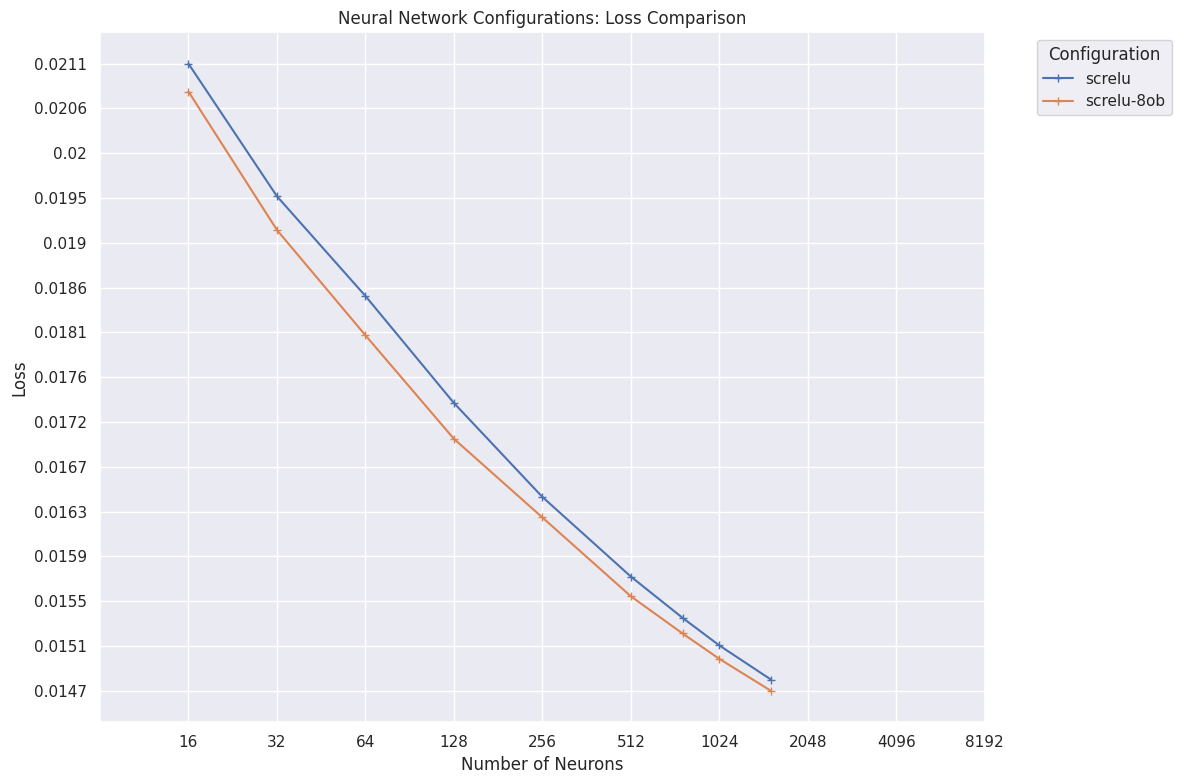
Final losses achieved after 10 superbatches with and without material output buckets.

Different learning rate schedules appear essentially indistinguishable, with cosine decay potentially edging the others out:

Final losses achieved after 10 superbatches with different learning rate schedules.

Well, that's all. Thanks for reading!