Better activation functions for NNUE

Swish

Viridithas 19's NNUE has four layers. L₀ is activated with pairwise-multiplied clipped ReLUAs mentioned in the previous post, this is a GLU variant. ↩, L₁ and L₂ with squared clipped ReLU, and L₃ with the sigmoid.

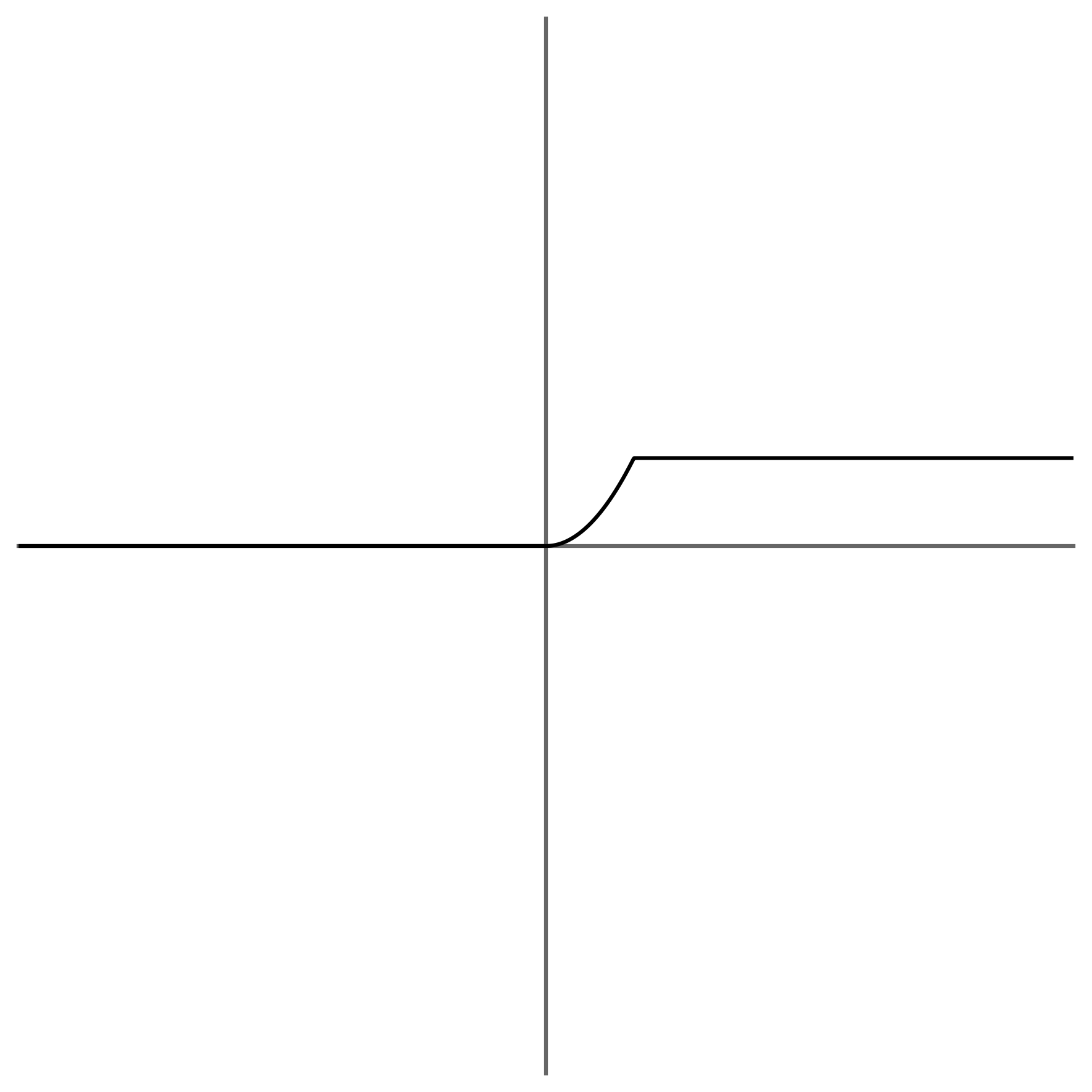
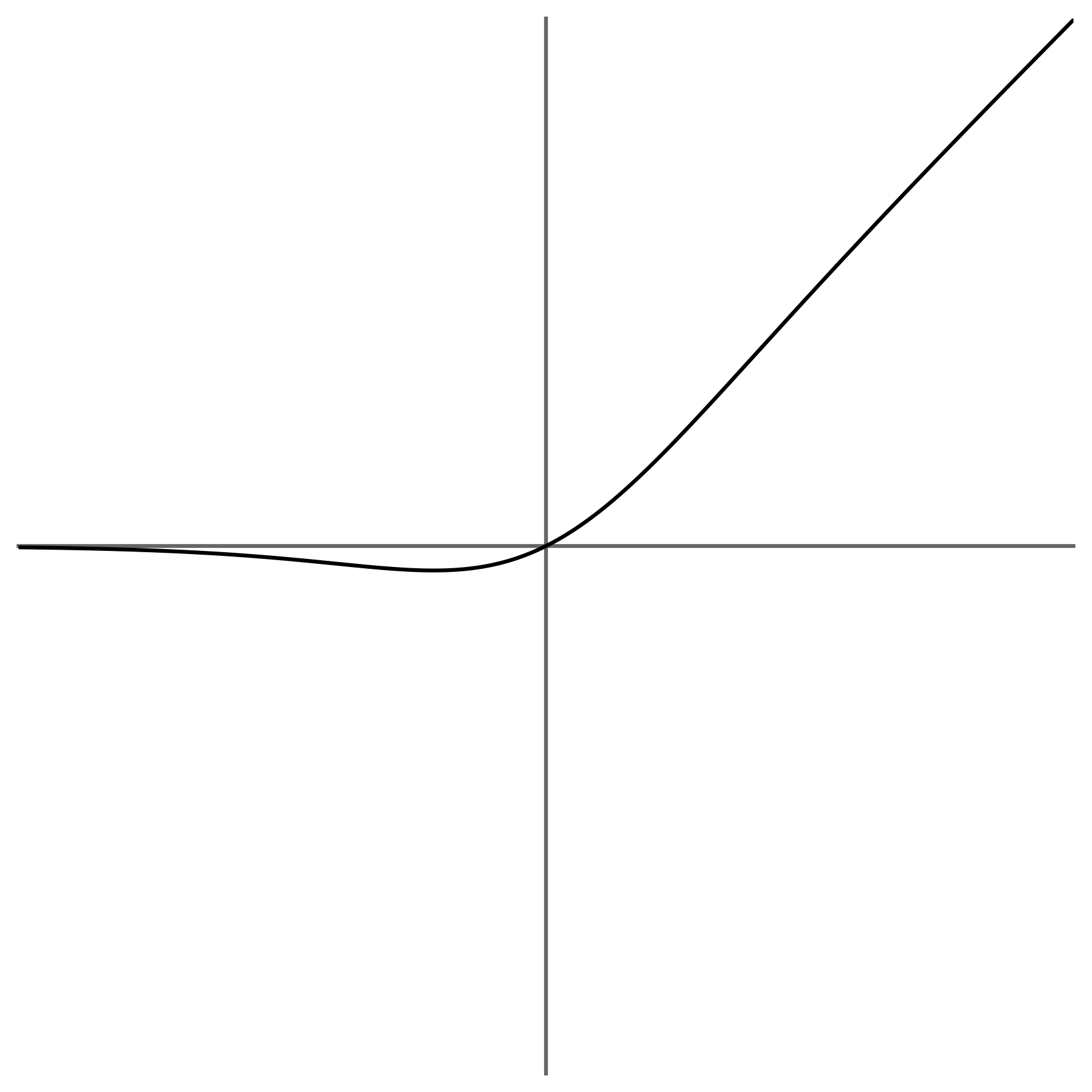
I originally wanted to experiment with modifications of the GLU in the first layer, but it is far easier to search under the street-light, and so I instead performed the experiment of replacing the SCReLUs on L₁ and L₂ with Swish. When doing this, I was yet to come across the well-vectorising $e^x$ approximationA good treatment of approximations to $e^x$ can be found at https://expositor.dev/approximation ↩ in A Fast, Compact Approximation of the Exponential Function by Nicol Schraudolph, and so I used the Hard-Swish approximationInvented in Searching for MobileNetV3. ↩ instead, with a fixed $\beta = ⅙$.

$$\begin{aligned} \mathrm{SCReLU}(x) &= \mathrm{clamp}(x, 0, 1)^2 \\ \mathrm{Swish}(x) &= x \cdot \sigma(\beta x) \\ \mathrm{Hard\text{-}Swish}(x) &= x \cdot \mathrm{clamp}(\beta x + 1/2, 0, 1) \end{aligned}$$

SCReLU

Swish

Hard-Swish

Teething problems

As explained in the article on deep NNUEs, Viridithas makes use of sparse matrix multiplication in L₁, with very significant implications for performance. Disastrously, the first network trained with Hard-Swish had a much lower sparsity in the L₀ output activations than usual, leading to a dramatic loss of performance in inference. The unit of sparsity in the L₁ matmul is a block of four adjacent u8-quantised activations - and with the introduction of Hard-Swish, block-sparsity fell from 70% to 50%.

Why might this be? One hypothesis is that, unlike SCReLU, Hard-Swish is unbounded from above. If you'll permit some hand-waving - it seems plausible that the ability for activations to grow without bound means that it can be useful for larger numbers of neurons to “work together” to push an activation in L₁ further upward, leading to more dense activations. There are issues with this explanation - if you want large activations, why not just increase the size of the weights? - but I lack any better ideas, and so hand-waving will have to satisfy us for now.

Regularisation to the rescue

Thankfully, the problem of activation density admits a very obvious solution - just directly penalise dense activations. We can do this by adding an additional term to the loss, minimising the L₁ norm of the activations in L₀’s output. A network trained with Hard-Swish and this regularisation term had a block-sparsity slightly exceeding that of the unregularised SCReLU networks, and so, from a performance perspective, all was well.

Smoothness

An interesting result of this activation change is that the evaluation scale of the network across the sample dataset used in the article on NNUE evaluation scale drift becomes far smoother.

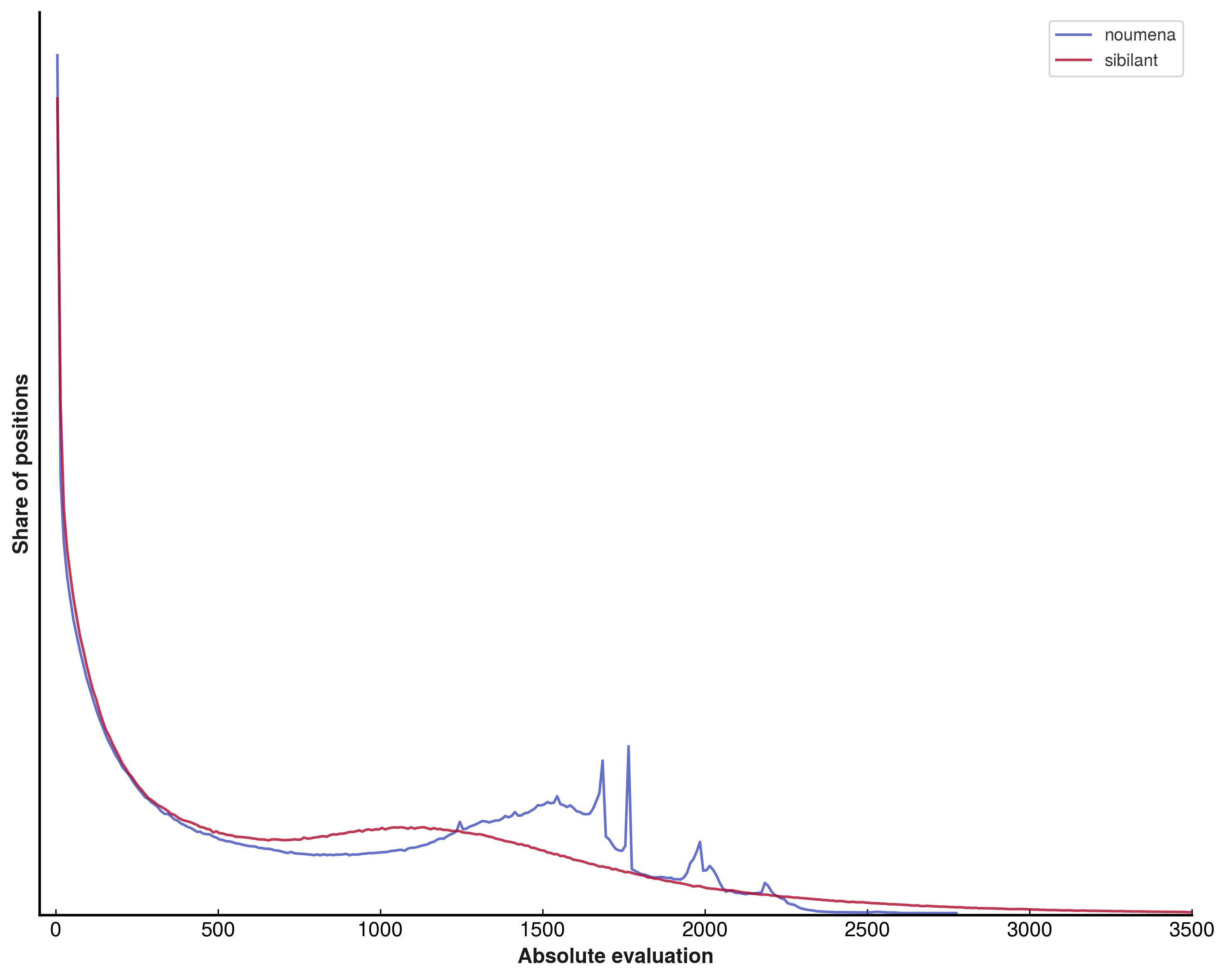
These networks make use of sparsely routed subnetworks in L₁, L₂, and L₃ - and breaking the histograms down by subnetwork is incredibly interesting:

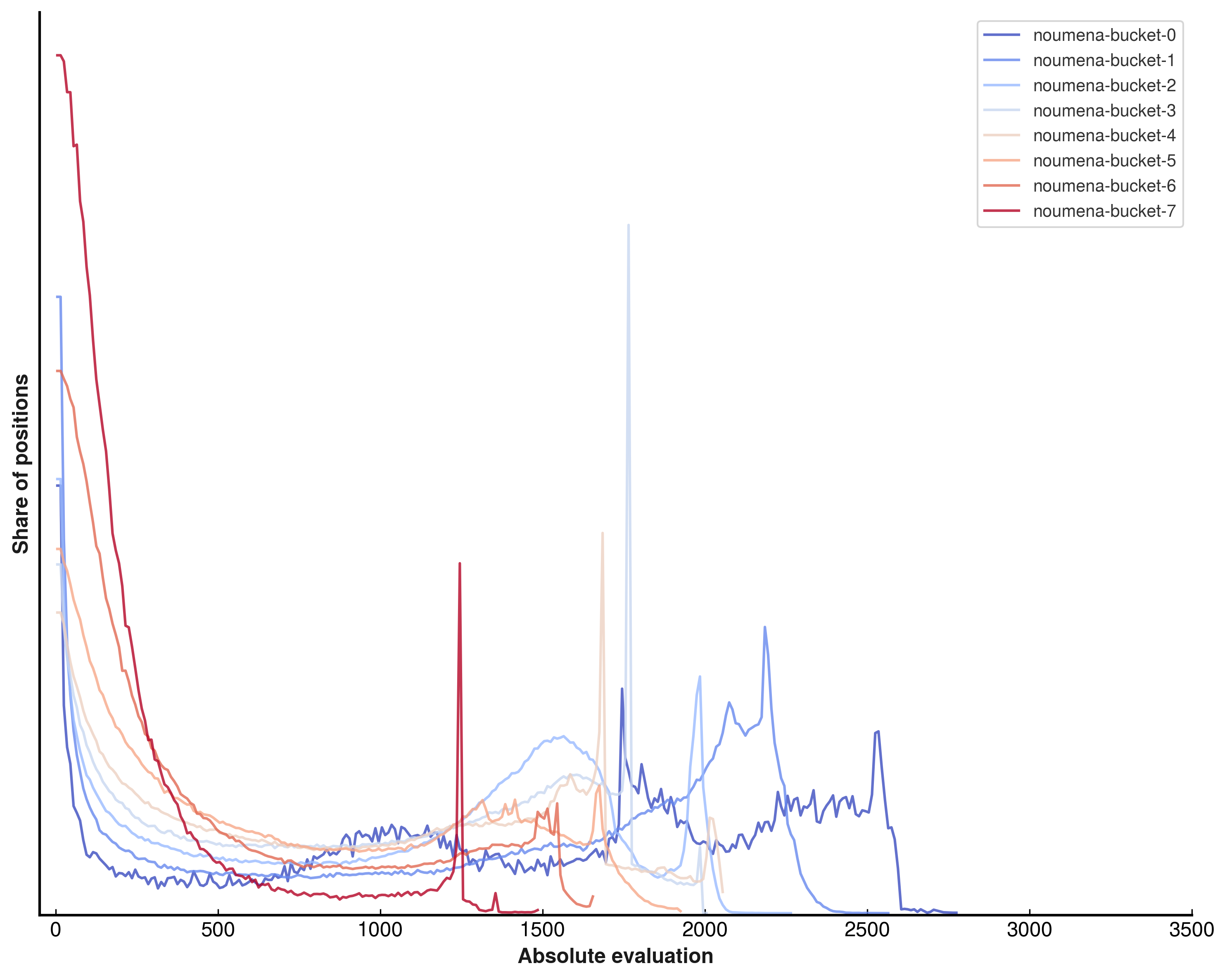
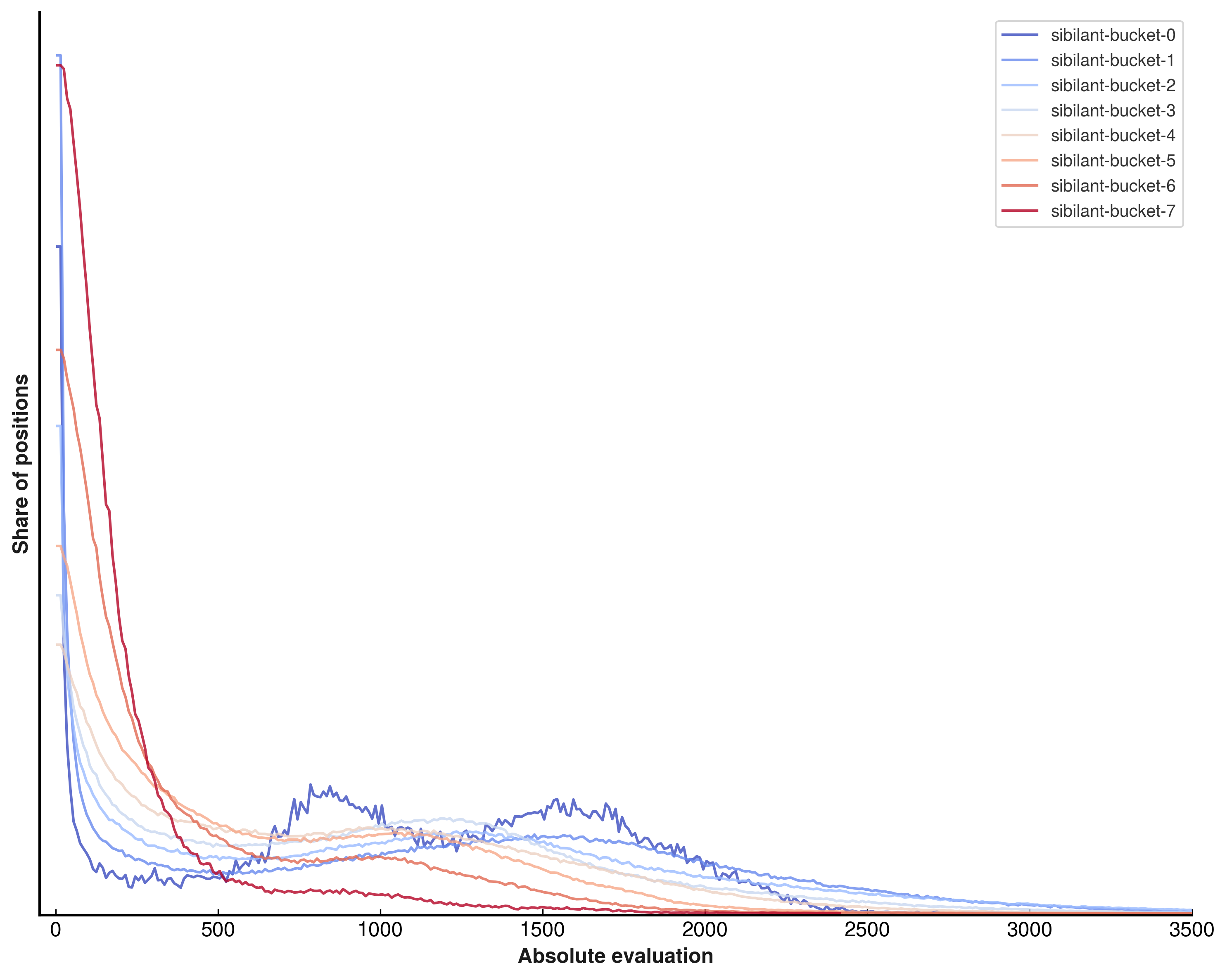
Strength improvements

The Swish network was tested for strength against the SCReLU baseline, gaining a great deal of Elo at both short and long time control:

  LLR +3.09 (−2.94LO +2.94HI BOUNDS for +0.00LO +3.00HI ELO)
  ELO +13.77 ± 5.04 (+8.74LO +18.81HI)
 CONF 8+0.08 SEC (1 THREAD 16 MB CACHE)
GAMES 5048 (1349W26.7% 2550D50.5% 1149L22.8%)
PENTA 28+2 703+1 1249+0 529−1 15−2

  LLR +3.04 (−2.94LO +2.94HI BOUNDS for +0.00LO +3.00HI ELO)
  ELO +5.90 ± 3.11 (+2.80LO +9.01HI)
 CONF 40+0.4 SEC (1 THREAD 128 MB CACHE)
GAMES 11660 (2918W25.0% 6022D51.6% 2720L23.3%)
PENTA 22+2 1437+1 3100+0 1259−1 12−2

These results should be placed in context - SCReLU on L₁ and L₂ was not necessarily the state of the art prior to this experiment - in a very strong enginehttps://github.com/Yoshie2000/PlentyChess ↩, the optimal activation functions were found to be CReLU on L₁ and SCReLU on L₂.

Additionally, Viridithas is somewhat unusual in not using weight clipping on the layers after L₁, which may also interact in a non-trivial manner with the activation functions used.

SwiGLU

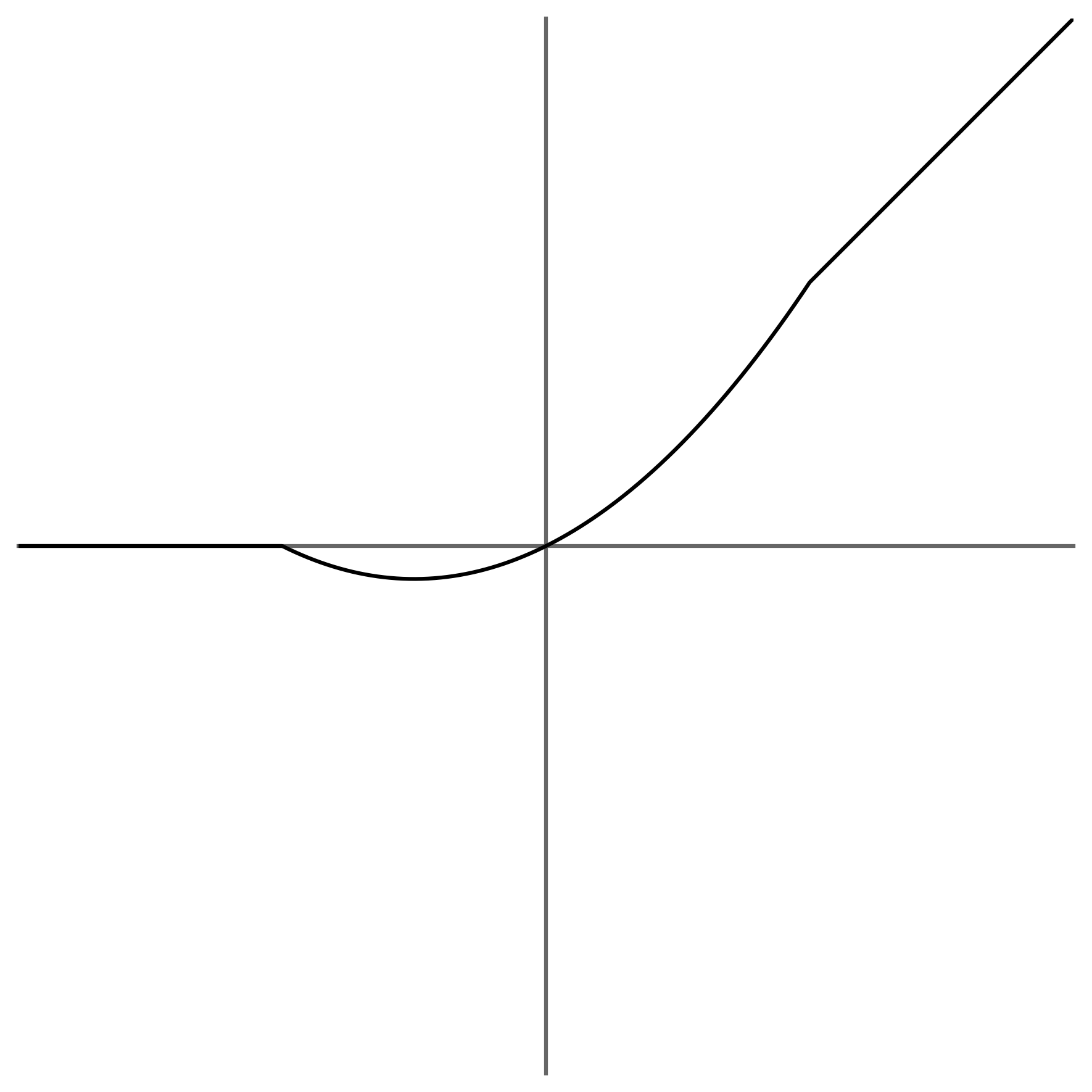
Encouraged by the success of Swish, I proceeded to replace Swish on L₂ with SwiGLUInvented in GLU Variants Improve Transformer. ↩.

$$\text{FFN}_\mathrm{SwiGLU}(x) = \text{Swish}(W_0 x) \otimes (W_1 x)$$

This change yielded further improvements in strength:

  LLR +2.95 (−2.94LO +2.94HI BOUNDS for +0.00LO +3.00HI ELO)
  ELO +5.47 ± 3.04 (+2.43LO +8.51HI)
 CONF 40+0.4 SEC (1 THREAD 128 MB CACHE)
GAMES 12578 (3131W24.9% 6514D51.8% 2933L23.3%)
PENTA 20+2 1597+1 3249+0 1407−1 16−2

and, for posterity, a nice output bucket histogram:

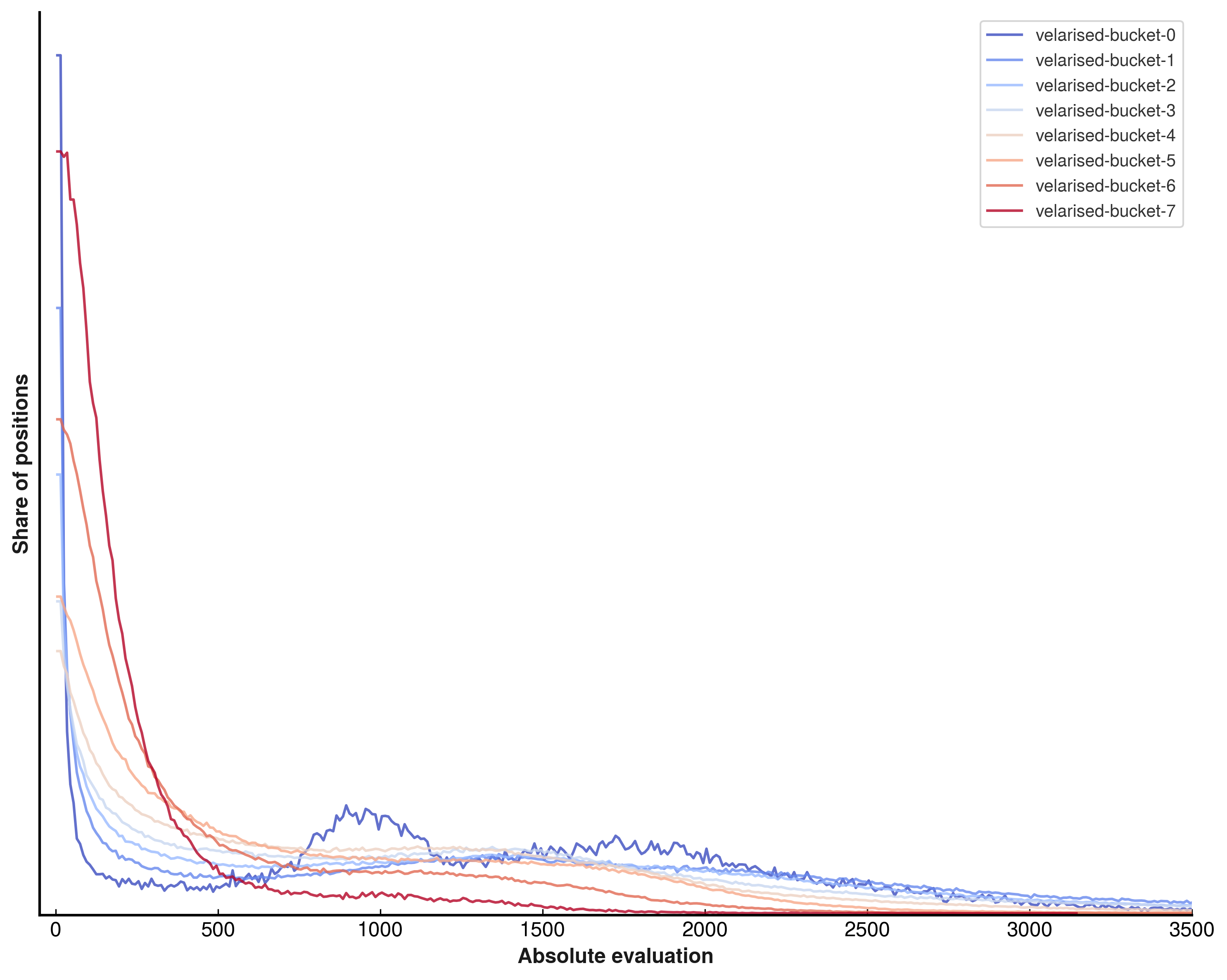
This means that Viridithas’s final activation sequence is:

$$\begin{aligned} L_0(x) &= \mathrm{clamp}(W_0 x, \mathbf{0}, \mathbf{1}) \otimes \mathrm{clamp}(W_1 x, \mathbf{0}, \mathbf{1}) \\ L_1(x) &= \mathrm{Hard\text{-}Swish}(W x) \\ L_2(x) &= \mathrm{Hard\text{-}Swish}(W_0 x) \otimes (W_1 x) \\ L_3(x) &= \sigma(W x) \end{aligned}$$

Interestingly, as Swish is sort of like a smooth ReLU, and SwiGLU with identical $W_0 = W_1$ is sort of like a smooth ReLU², this activation sequence is very reminiscent of the CReLU + SCReLU sequence that was found to be best for PlentyChess - which might mean something, or might just be co-incidenceThe author of PlentyChess thinks that it is co-incidence. ↩.

Conclusion

I've become a big fan of Swish and SwiGLU as activation functions for NNUE. More than this, I've become very excited about more broadly integrating the wisdom of the deep learning community into chess NNUE design. Future posts may explore other ideas, like expert mixing, learned routing, factored matrixes for structured sparsity, categorical value prediction, recurrence, and weight sharing. See you then!